Probability is a tricky subject with a lot of concepts that are not easy to grasp and understand. However, it is also among the few mathematical concepts that the average person is likely to use regularly in life. Whether it is while flipping a coin, entering a lottery, or playing your favourite board game, probability helps you make sense of the world through the prism of pure mathematics. However, people often conflate probability with being a simple game of fractions.
As any statistician or mathematician would emphatically tell you, there is nothing further from the truth. Probability, even at moderate levels, can borrow from multiple advanced mathematical concepts, such as permutations and combinations and the set theory. These concepts help solve complex problems such as the forecasting of stock markets, preempting election results, and understanding trading patterns throughout the world.
A fundamental concept that permeates through all of probability is the concept of sample space. However, high school students, when they are first acquainted with probability, are not explained this concept exhaustively. There are many more facets to the seemingly simple idea of sample space in probability, and this article attempts to lay out these facets. Several questions will be attempted to be answered by way of this article. Some of these questions are as follows.
What is sample space?
What are the conditions of a sample space?
What are the different types of sample spaces?
Sample Space
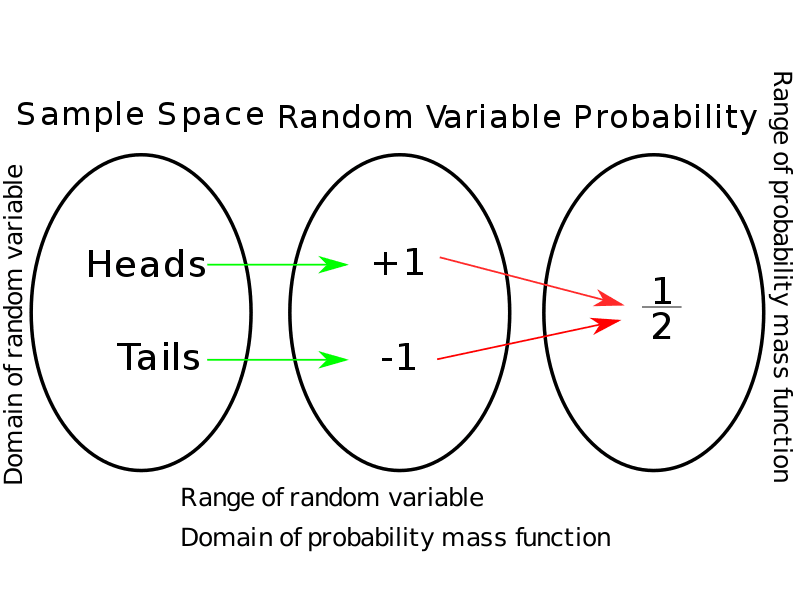
Put very simply, in an experiment, a sample space is the set of all outcomes of the investigation. A sample space is also known as a possibility space or a sample description space. The way to denote the sample space in probability theory is using a set. The elements of this set are all the possible outcomes of the experiment being conducted. There aren’t a lot of restrictions on what type of factors may be included in a sample space. This mostly depends on the kind of results the experiment being conducted yields.
The simplest example that can be used to explain the concept of a sample space is the tossing of two coins together. When you toss two coins, there are four types of outputs that you can get – –two heads, two tails, a head and a tail, and a tail and a head. These four outcomes are your sample space -if your sample space is to be denoted by the letter S, the S = {HH, HT, TH, TT}.
Each element of the sample space set is known as an event. It is essential in any problem related to probability that the sample space is well defined and understandable. According to probability theory, there are three crucial elements of a probabilistic model. These three elements are a well-defined sample space, a well-defined set of events in the sample space, a distinct probability assigned to each occurrence of the sample space.
Hence, having a clear knowledge of your sample space increases the chance that your probabilistic model will be successful.
The Conditions of a Sample Space
Certain conditions bound the definition of a sample space. This means that an arbitrary set can only be called a sample space if it meets certain requirements. These conditions are as follows.
- The event contained in a sample space must necessarily be mutually exclusive. This means that only one event may occur at a particular point in time, and if one event takes place, no other can.
- The events contained in the sample space are completely exhaustive. This means that the sample space of a random trial must have all the possible outcomes of that random trial. There must not occur such a situation that a random experiment is conducted and the product is not a part of the sample space.
- The events included in the sample space must contain the right granularity. This means that the sample space must have no such information that is irrelevant to the outcome of the random experiment. For example, the sample space when a die is thrown is {1, 2, 3, 4, 5, 6}. However, another prospective sample space is {1 and sunshine, 1 and no sunshine, 2 and sunshine, 2 and no sunshine, 3 and sunshine, 3 and no sunshine, 4 and sunshine, 4 and no sunshine, 5 and sunshine, 5 and no sunshine, 6 and sunshine, 6 and no sunshine}. Here, the outcome of the experiment of throwing a die is not changed by the presence of sunshine, so there is no need to include that information in the sample space.
One Experiment, Multiple Sample Spaces
Can there be multiple sample spaces associated with the same experiment? This depends on the type of random trial that is being conducted. It also depends on the information that the experimenter is looking for. Say the experiment has multiple facets and the experimenter is looking for just the probability of one of those elements. There can sure be multiple sample spaces related to the same experiment. However, the exhaustive sample space will still be the one that contains all the outcomes of the investigation.
As an example, we may take the drawing of a card from a deck of cards. Each card of the deck has two components – the denomination of the card, and the suit of the card. If the experimenter in question is conducting an experiment where the primary outcome is the card denomination, the sample space of the investigation is {A, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K}.
However, if the experimenter in question is conducting an experiment where the primary outcome is the card suit, the sample space of the investigation is {spade, heart, diamond, club}. A completely exhaustive sample space of each of these experiments will still be the Cartesian product of these two sets. Still, since one has no impact on the other as far as the individual experiments are concerned, the sample spaces mentioned above may be used.
The Role of Sample Space in Measuring Probability
Now that we know what a sample space is, the question arises – what is the role of a sample space in the probability theory? Why is it considered such an essential component of any probabilistic model?
The elementary theory of probability assumes that the random trial conducted is fair. Suppose the sample space has been defined according to the conditions that restricts its definition. In that case, every event of the sample space has an equal probability of occurring. This means that the probability of each event in the sample space is equal to the reciprocal of the number of events in the samples space. It is important to note here that not all experiments have equally likely outcomes. For example, the likelihood of a head and a tail in a biased coin will not be equal.
When the outcomes are equally likely, the calculation of the probability of events that comply with specific conditions in the sample space becomes very easy. All the calculator now needs to do is count the number of events in the sample space that follow the condition mentioned above, and divide it by the total number of events.
For example, say you want to calculate the probability of drawing a card between 3 and 5 from a deck of cards. The number of favourable outcomes from the first set mentioned in the previous section is 3. The total number of outcomes is 13. The probability is hence equal to 3/13.
Conclusion
The concept of sample space is significant in probability and among the three pillars on which any probabilistic model stands. This article aimed to acquaint readers with the intricacies of the sample space concept. It explained the definition of samples space, followed by the conditions to be met for calling a set a sample space. It then moved on to the concept of multiple sample spaces from the same experiment. It ended with the role of the sample space concept in probability theory.
Probability is used in several data handling concepts, and you may use any of the number of online resources available to understand data handling and interpretation and conduct more advanced studies in it. Data is the future, and you must grab all opportunities you get to learn about it.

Be the first to comment